Power Plots in statsmodels

I just want to show another two plots for the statistical power of a test, since I didn't have time for this earlier

The code to produce them is just calling the methods of the power classes, for example for the one sample t-test.

Polar Histogram

Just posting two plots from my gallery to show what we can do with matplotlib, and numpy and scipy. (No public code for now)
Both plots show the histogram of the data and the density function (pdf) of the Von Mises distribution with estimated mu and kappa.
The first one shows arrival times in a 24 hour clock

The second one shows wind direction (zero is north, I didn't use the offset in this plot.)

Regression Plots - Part 1

I started to work on improving the documentation for the regressions plot in statsmodels. (However, I realized I have to improve them a bit.)

For now, just a question: Can you spot the mis-specification of the model?

I simulate a model, run a linear regression on three variables and a constant. Here is the estimation summary, which looks quite good, large R-squared, all variables significant, no obvious problems:

>>> print res.summary()
                                                        OLS Regression Results
==============================================================================
Dep. Variable:                      y   R-squared:                       0.901
Model:                            OLS   Adj. R-squared:                  0.898
Method:                 Least Squares   F-statistic:                     290.3
Date:                Thu, 10 May 2012   Prob (F-statistic):           5.31e-48
Time:                        13:15:22   Log-Likelihood:                -173.85
No. Observations:                 100   AIC:                             355.7
Df Residuals:                      96   BIC:                             366.1
Df Model:                           3
==============================================================================
                 coef    std err          t      P>|t|      [95.0% Conf. Int.]
------------------------------------------------------------------------------
x1             0.4872      0.024     20.076      0.000         0.439     0.535
x2             0.5408      0.045     12.067      0.000         0.452     0.630
x3             0.5136      0.030     16.943      0.000         0.453     0.574
const          4.6294      0.372     12.446      0.000         3.891     5.368
==============================================================================
Omnibus:                        0.945   Durbin-Watson:                   1.570
Prob(Omnibus):                  0.624   Jarque-Bera (JB):                1.031
Skew:                          -0.159   Prob(JB):                        0.597
Kurtosis:                       2.617   Cond. No.                         33.2
==============================================================================

The following three graphs are refactored versions of the regression plots. Each graph looks at the data and estimation results with respect to one of the three variables. (The graphs look better in original size.)
The short lines in the first subplot of each graph are the prediction confidence intervals for each observation.
The code is short, if we have the (still unpublished) helper functions.
res is an OLS results instance

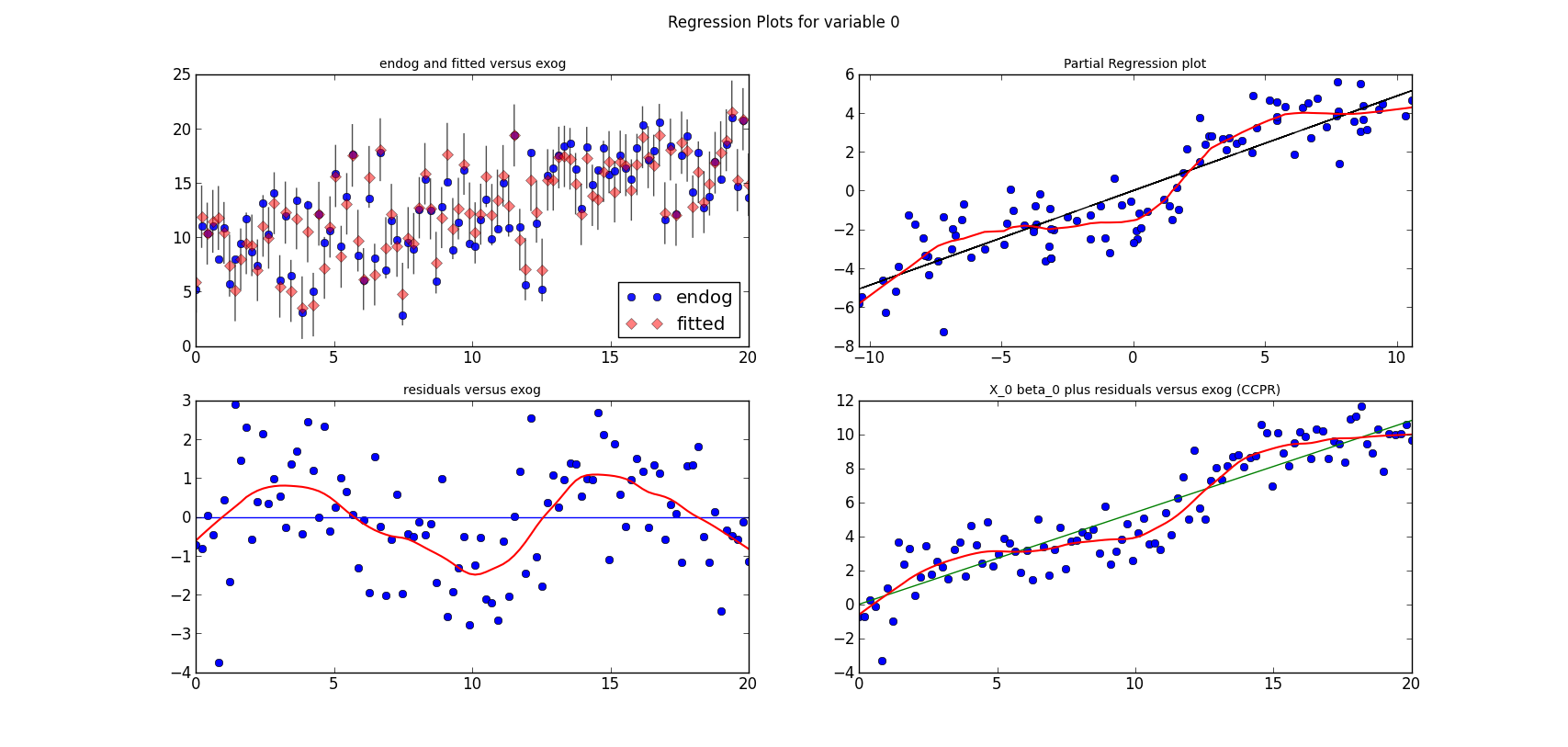
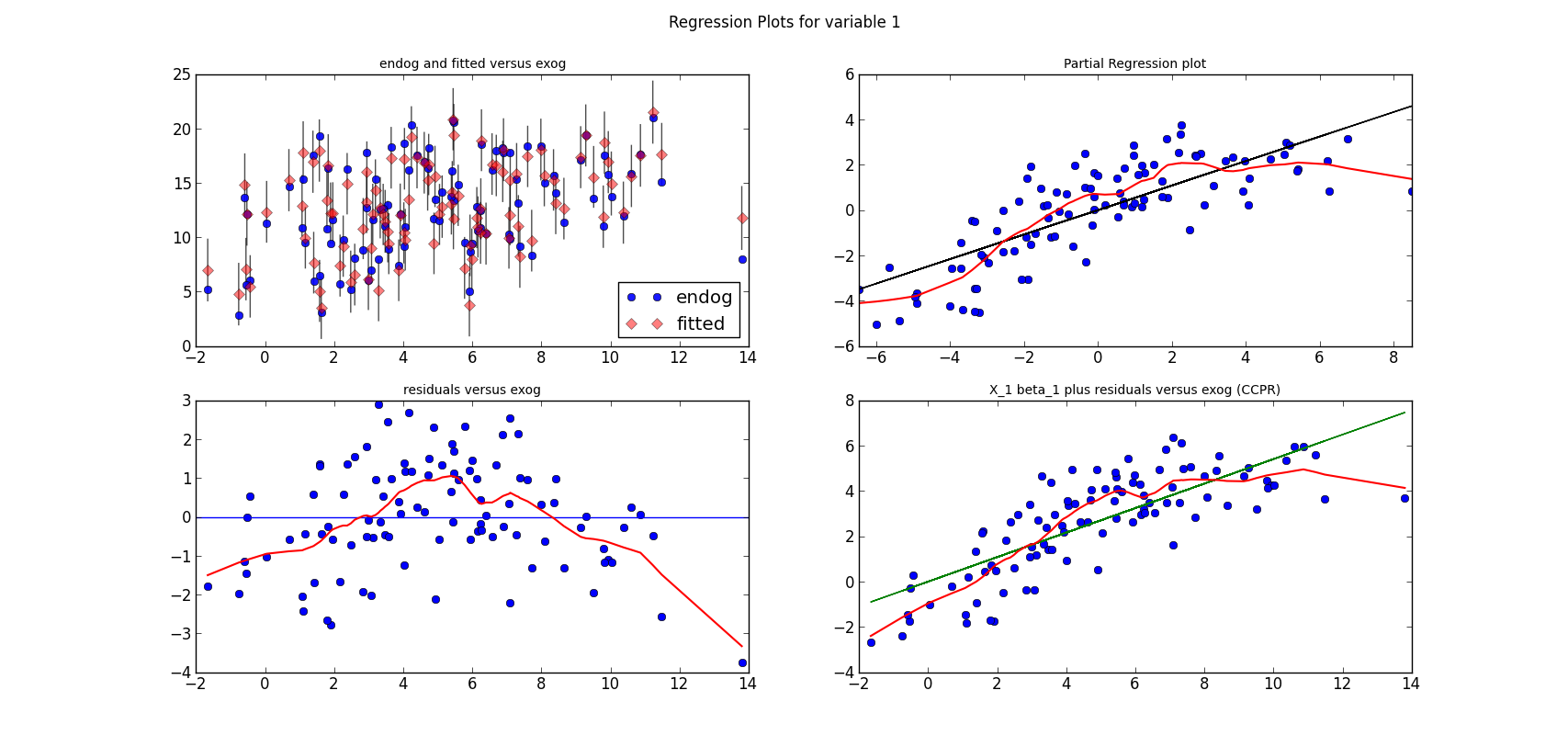
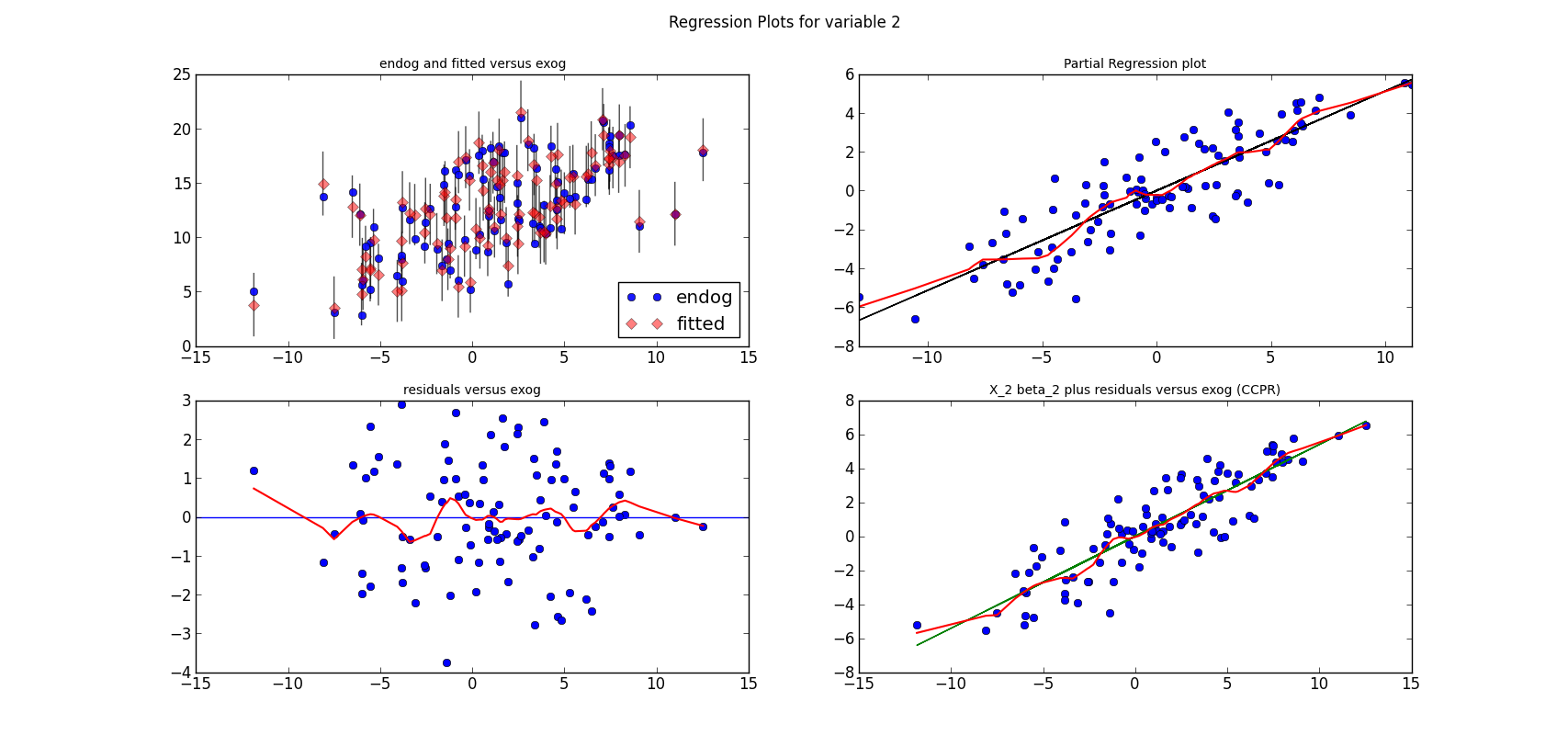
from regressionplots_new import plot_regress_exog

fig9 = plot_regress_exog(res, exog_idx=0)
add_lowess(fig9, ax_idx=1, lines_idx=0)
add_lowess(fig9, ax_idx=2, lines_idx=0)
add_lowess(fig9, ax_idx=3, lines_idx=0)

fig10 = plot_regress_exog(res, exog_idx=1)
add_lowess(fig10, ax_idx=1, lines_idx=0)
add_lowess(fig10, ax_idx=2, lines_idx=0)
add_lowess(fig10, ax_idx=3, lines_idx=0)

fig11 = plot_regress_exog(res, exog_idx=2)
add_lowess(fig11, ax_idx=1, lines_idx=0)
add_lowess(fig11, ax_idx=2, lines_idx=0)
add_lowess(fig11, ax_idx=3, lines_idx=0)

Plots in statsmodels: qqplot

Other news first, since I haven't managed to catch up with the blogs:

• statsmodels has four students in GSoC, the first four projects described in my previous post. Congratulations to Alexandre, Divyanshu, George and Justin
• statsmodels 0.4.0 has been release with new name without scikits in front, more on pypi

statsmodels has a graphics subdirectory, where we started to collect some of the common statistical plots. To make the documentation a bit more exciting, I am adding plots directly to the docstrings for the individual functions. Currently, we don't have many of them in the online documentation yet, two examples violin_plot and bean_plot.
A note on the documentation: Skipper improved the frontpage, which makes it easier to find the documentation for the latest released version and for the development version. Currently, the development version is better and is improving, and it is incompatible with the 0.4.0 release in only one part.

quantile-quantile plot: qqplot

The documentation for the function is here. The function signature is

qqplot(data, dist=stats.norm, distargs=(), a=0, loc=0, scale=1, fit=False, line=False, ax=None)

I am not copying the entire docstring, what I would like to present here are some examples and how to work with the plots.
The first example is from the docstring. I don't like the default, so I kept adding keyword arguments until the plot is more to my taste.

• The first plot uses no keywords and assumes normal distribution, and does not standardize the data.
• The second plot adds line='s', which according to the docstring

  's' - standardized line, the expected order statistics are scaled
        by the standard deviation of the given sample and have the mean
        added to them
  

  corresponds to the line after fitting location and scale for the normal distribution
• The third plot adds fit=True to get standardized sample quantiles and plots the 45 degree line. That's the plot I would prefer.
• The fourth plot is similar to the third plot, but with the t distribution instead of the normal distribution. I was surprised that the third and fourth plot look the same, until I checked and it turned out that the fitted t distribution has a huge degrees of freedom parameter and so is essentially identical to the normal distribution.

I will go over the code to produce this below.
I started the second example to see whether fitting the t distribution works correctly. Instead of using real data, I generate 1000 observations with a t distribution with df=4 and standard location(0) and scale (1).

• The first plot fits a normal distribution, keywords: line='45', fit=True
• The second plot fits the t distribution, keywords: dist=stats.t, line='45', fit=True
• The third plot is the same as the second plot, but I fit the t distribution myself, instead of having qqplot do it. keywords: dist=stats.t, distargs=(dof,), loc=loc, scale=scale, line='45'. I added the estimated parameters into a text insert in the plot. qqplot currently doesn't tell us what the fitted parameters are.

The Code

Here was my first attempt, following the docstring example

from scipy import stats
import statsmodels.api as sm

#estimate to get the residuals
data = sm.datasets.longley.load()
data.exog = sm.add_constant(data.exog)
mod_fit = sm.OLS(data.endog, data.exog).fit()
res = mod_fit.resid

fig = sm.graphics.qqplot(res, dist=stats.t, line='45', fit=True)
fig.show()

It works but the x-axis goes from -3 to 3, while there are only values from -2 to 2.

Detour to some background

A while ago we had a discussion on the mailing list what a plot in statsmodels should return. With the helpful comments of John Hunter, we finally agreed that plots should take an ax (matplotlib axis) argument if it's meaningful, and always return a figure instance fig. If ax is None, or the plot is a combination plot (several plots in one figure), then a figure is created and returned. If ax is given, then that is used to attach the plot elements. Ralf Gommers converted our plot functions to follow this pattern, besides that, he also wrote several of the plots that are currently in statsmodels.
So, to change the axis limits in the above graph, all I have to add is:

fig.axes[0].set_xlim(-2, 2)

The resulting plot is then the same as the third plot in the first graph above.

The first graph

Here is now the script for the first graph in several stages:
First I import some modules and calculate the residuals following the example

from scipy import stats
from matplotlib import pyplot as plt
import statsmodels.api as sm

#example from docstring
data = sm.datasets.longley.load()
data.exog = sm.add_constant(data.exog)
mod_fit = sm.OLS(data.endog, data.exog).fit()
res = mod_fit.resid

Then I hardcode a left position for text inserts, and create a matplotlib figure instance

left = -1.8
fig = plt.figure()

Next we can add the first subplot. The only keyword arguments for qqplot is ax to tell qqplot to attach the plot to my first subplot. Since I want to insert a text to describe the keywords, I needed to spend some time with the matplotlib documentation. As we have a reference to the axis instance, it is easy to change or add plot elements

ax = fig.add_subplot(2, 2, 1)
sm.graphics.qqplot(res, ax=ax)
top = ax.get_ylim()[1] * 0.75
txt = ax.text(left, top, 'no keywords', verticalalignment='top')
txt.set_bbox(dict(facecolor='k', alpha=0.1))

The other subplots follow the same pattern. I didn't try to generalize or avoid hardcoding

ax = fig.add_subplot(2, 2, 2)
sm.graphics.qqplot(res, line='s', ax=ax)
top = ax.get_ylim()[1] * 0.75
txt = ax.text(left, top, "line='s'", verticalalignment='top')
txt.set_bbox(dict(facecolor='k', alpha=0.1))

ax = fig.add_subplot(2, 2, 3)
sm.graphics.qqplot(res, line='45', fit=True, ax=ax)
ax.set_xlim(-2, 2)
top = ax.get_ylim()[1] * 0.75
txt = ax.text(left, top, "line='45', \nfit=True", verticalalignment='top')
txt.set_bbox(dict(facecolor='k', alpha=0.1))

ax = fig.add_subplot(2, 2, 4)
sm.graphics.qqplot(res, dist=stats.t, line='45', fit=True, ax=ax)
ax.set_xlim(-2, 2)
top = ax.get_ylim()[1] * 0.75
txt = ax.text(left, top, "dist=stats.t, \nline='45', \nfit=True",
              verticalalignment='top')
txt.set_bbox(dict(facecolor='k', alpha=0.1))

The final step is to adjust the layout, so that axis labels don't overlap with other subplots if the graph is not very large

fig.tight_layout()

The second graph

The second graph follows the same pattern with a few changes.
First we generate a random sample using scipy.stats which under the hood uses the random numbers from numpy. You can notice here that I am cheating. I ran the script several times to find "nice" seeds. Especially in smaller samples, qqplot might often not be very good in distinguishing normal and t distributions.

import numpy as np
seed = np.random.randint(1000000)
print 'seed', seed
seed = 461970  #nice seed for nobs=1000
#seed = 571478  #nice seed for nobs=100
#seed = 247819  #for nobs=100, estimated t is essentially normal
np.random.seed(seed)
rvs = stats.t.rvs(4, size=1000)

The first two subplot are very similar to what is in the first graph

fig2 = plt.figure()
ax = fig2.add_subplot(2, 2, 1)
fig2 = sm.graphics.qqplot(rvs, dist=stats.norm, line='45', fit=True, ax=ax)
top = ax.get_ylim()[1] * 0.75
xlim = ax.get_xlim()
frac = 0.1
left = xlim[0] * (1-frac) + xlim[1] * frac
txt = ax.text(left, top, "normal", verticalalignment='top')
txt.set_bbox(dict(facecolor='k', alpha=0.1))

ax = fig2.add_subplot(2, 2, 2)
fig2 = sm.graphics.qqplot(rvs, dist=stats.t, line='45', fit=True, ax=ax)
top = ax.get_ylim()[1] * 0.75
xlim = ax.get_xlim()
frac = 0.1
left = xlim[0] * (1-frac) + xlim[1] * frac
txt = ax.text(left, top, "t", verticalalignment='top')
txt.set_bbox(dict(facecolor='k', alpha=0.1))

For the third plot, I estimate the parameters of the t-distribution to see whether I get the same results as in the second plot (I do), and so I can insert the parameter estimates into the plot

params = stats.t.fit(rvs)
dof, loc, scale = params
ax = fig2.add_subplot(2, 2, 4)
fig2 = sm.graphics.qqplot(rvs, dist=stats.t, distargs=(dof,), loc=loc,
                 scale=scale, line='45', fit=False, ax=ax)
top = ax.get_ylim()[1] * 0.75
xlim = ax.get_xlim()
frac = 0.1
left = xlim[0] * (1-frac) + xlim[1] * frac
txt = ax.text(left, top, "t \ndof=%3.2F \nloc=%3.2F, \nscale=%3.2F" % tuple(params),
              verticalalignment='top')
txt.set_bbox(dict(facecolor='k', alpha=0.1))

That's it for the plots, now I need to add them to the statsmodels documentation.

PS: normality tests, details left for another day

qqplots give us a visual check whether a sample follows a specific distribution. The case that we are interested in most often, is a test for normality. Scipy.stats and statsmodels have several normality tests. The ones I have written recently are Anderson-Darling and Lillifors. Lillifors is a Kolmogorov-Smirnov test for normality when mean and variance are estimated. Calculating a statistical test provides a more reliable test than a "vague" visual inspection, but these tests do not point us to a specific alternative and provide less information about the direction in which a null hypothesis might be incorrect.
Using the residuals in the first example, neither test rejects the Null Hypothesis that the residuals come from a normal distribution

>>> normal_ad(res)
(0.43982328207860633, 0.25498161947268855)
>>> lillifors(res)
(0.17229856392873188, 0.2354638181341876)

On the other hand, in the second example with 1000 observations from the t distribution, the assumption that the data comes from a normal distribution is clearly rejected

>>> normal_ad(rvs)
(6.5408483355136013, 4.7694160497092537e-16)
>>> lillifors(rvs)
(0.05919821253474411, 8.5872265678140885e-09)

PPS:
I'm reluctant to publish the import path, because I had forgotten to add them to a proper place for 0.4.0, and the import location will not stay where it is. It took me a few minutes to find out that they are not on any recommended import path when I wrote these scripts

>>> from statsmodels.stats.adnorm import normal_ad
>>> from statsmodels.stats.lilliefors import lillifors

Distributions with matplotlib in 3d

I finally managed to figure out the settings for matplotlib's surface plot that makes a bivariate distribution look more like those in published articles.

The first version uses

ax2 = fig2.add_subplot(111, projection='3d')
surf = ax2.plot_surface(X, Y, Z, rstride=1, cstride=1, 
        cmap = cm.gray_r, alpha=0.9, linewidth=1)

The second version uses

surf = ax.plot_surface(X, Y, Z, rstride=1, cstride=1, color='0.8',
                       alpha=0.85, linewidth=1)

Previously I was trying out mainly the contour plots, since I didn't get 3d to look nice enough.

For example the following shows a mixture of two bivariate normal distributions and the estimate by gaussian_kde. The colored areas are the differences between kde and the true distribution, in the blue areas the kde is too large, in the redish areas the kde is too small. It's a contour plot version for showing that gaussian_kde with default settings for the bandwidth lowers the hills and fills the valleys in the case of bimodal distributions.